證明者演算法可以分成五輪,現在就由第一輪開始,其中證明者計算線多項式,然後並提交給驗證者。
但在此之前,需要回到KZG並解決一些尚未解決的問題。具體來說,將展示誰產生評估挑戰以及如何隱藏多項式評估以獲得零知識協議。
第一輪的步驟:
產生一組隨機綁定的標量
計算線多項式: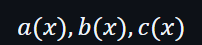
計算及產出證明: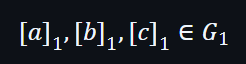
在描述 KZG 時,當中的挑戰是以某種方式給出的。在交互式情況下,該值可以由驗證者發出,但我們的目標是非交互式協議。
將交互式協定轉換為非交互式協定可以透過 Fiat-Shamir 來完成,這表示證明者使用隨機預言機及自行計算所有挑戰。
所產出的預言可能是加密雜湊函數 H ,而 H 可以接受可變長度輸入及會得出一個固定長度輸出。
重要的屬性是:
當證明者需要被驗證者挑戰時,可以去查詢預言機 H 某些輸入值。在 PlonK 下,向預言機 H 的輸入會是一個協議記錄。
可以把它理解為以下部分組成的協議的總結:
驗證者也可以存取隨機預言。由於它是確定性的及相關的記錄是公開的,驗證者可以在驗證階段重組相關挑戰。
這種啟發式有一些需要注意的安全假設。
驗證者如何知道證明者在選擇挑戰時沒有作弊?
根據協議,證明者可以查詢隨機預言機以獲得挑戰。但是有什麼阻止他自己選擇合適的挑戰呢? KZG 的驗證階段主要檢查: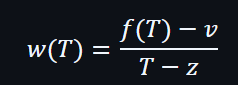
然而,如果證明者試圖偽造證明和計算出證人 w(τ) 和使用 y 來計算出評估 v=f(z)。
這不是由我們得到的隨機預言所決定的: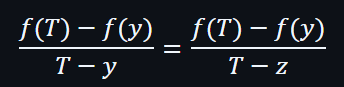
數值 T, z 都是固定值的,因為 T 由 SRS 的生成決定,而 z 由隨機預言機決定。
這意味著我們正在檢查兩個不同多項式在點 z1 的相等性。此檢查成功的機率可以忽略不計。
結果是不可能欺騙協議,因為驗證者可以檢索挑戰 z 從隨機預言檢視多項式在打開點的運算結果的有效性。
重溫 PlonK 圖
可以重申 PlonK 協議的圖表並且更加詳細。在證明者演算法的每一輪中,
都會基於已經完成計算的資料來創建多項式。最後證明者發送證明 π,
由隨機預言機取得的挑戰所得出的多項式承諾和多項式評估組成。
由於多項式承諾方案,驗證者可以驗證打開點的有效性,及執行驗證者演算法中描述的檢查。
綁定關係
到目前為止,我們已經討論了非零知識的普通 KZG 多項式承諾方案。
打開一個在挑戰的一個點的一個承諾多項式,會展示到有關該多項式的信息。然而在這裡的目標是使協議成為零知識,
因此在過程中是不會洩露任何相關資訊。
通過改變KZG,使證明者可以讓驗證者相信評估的有效性,但驗證者不會知道真正的評估內容。
為了實現這一目標,將使用綁定標量和零多項式。
考慮一個多項式 f(x) 在被預言機選擇的挑戰的點上打開。
PlonK 論文協議就建議以隨機的綁定標量來修改已提交的多項式:
假設綁定標量如下: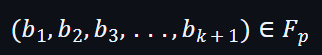
因此可以有以下公式:
綁定標量的數量應該會是至少比在f(x)上打開的數量增加1個。
由於x是在H內的元素,所以 f`(x) 會有包含一些 f(x)的資料。
然而,挑戰是由隨機預言機選擇的,這保證了它們是隨機選擇的。由於評估域的大小與次序的Fp域相比是較小,
選擇 H 內的隨機元素的機率是∣H∣/p,也會被認為是可以忽略不計。
如果選擇的挑戰不是來自 H,則多項式會被綁定化,很難從綁定化多項式中獲得原始多項式。
首先,要用以下等式來表示多項式承諾: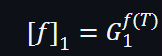
通過SRS形式,承諾將在多項式中的 T 點被評估及編碼為橢圓曲線的點,所以這個橢圓曲線的點會跟SRS是相對應的。
在第一輪,基本上是通過從計算表來創建一個多項式及提交出來,用於將證明者與見證人綁定起來,
同時透過應用拉格朗日插值及以綁定標量的形式增加隨機性,也將每一列作為線多項式的形式表示。
綁定標量由證明者隨機及獨立地進行抽取: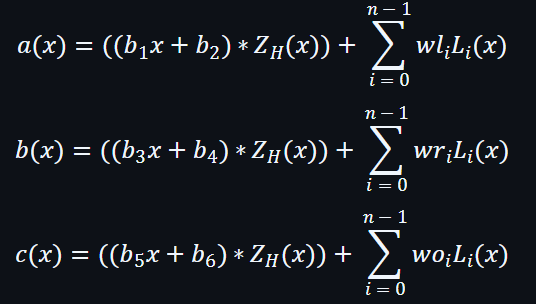
在完成創建以上的多項式後,證明者可以得到證明: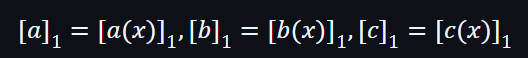
因此,在第一輪最後可以得出: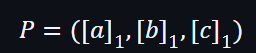
這個P的3個值是對應了算術表中的3個列,
然後用於KZG中。
